Fra CÆSAR til RSA

Oprindelsen til ordet kryptere er græsk, hvor det betyder skjult eller grotte. Kryptologi - læren om koder - handler om hvordan man kan kryptere meddelelser, men også om hvordan man kan bryde koder og vurdere sikkerheden.

Man kender krypteringssystemer, der er brugt helt tilbage i oldtiden og de er af samme type, som børn i dag selv finder på, når de skal sende hemmelige beskeder.

Cæsar udviklede et system, hvor han byttede om på alfabetets bogstaver, således at hvert bogstav i den oprindelige tekst blev erstattet med det bogstav, der står 3 pladser længere fremme i alfabetet. Således bliver Cæsar til Favdu.

Den tekst, der kommer ud af det, ser ved første øjekast helt umulig ud, men den skal ikke være ret lang før den kan tydes ved at se på hyppigheden af de forskellige bogstaver. Enhver, der har spillet "Scrabble" ved, hvor let det er at placere et E - det giver heller ingen points - og hvor svært det er at placere et X, der til gengæld giver 8 points. Denne pointgivning følger nøje bogstavfordelingen i en vilkårlig dansk tekst, der vil se nogenlunde sådan ud (i procent).

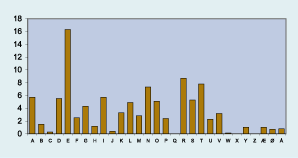
Er der byttet om på alfabetets bogstaver, vil der blot blive byttet om på søjlerne i diagrammet, men den højeste søjle vil sikkert afsløre E, den næsthøjeste R, etc. Et krypteringssystem, hvor man blot bytter om på bogstaverne er således ikke til megen nytte.

Der er i tidens løb udvist stor opfindsomhed for at undgå den store forekomst af E, men først med Vigenére (1586) opnåede man en rimelig sikkerhed. I Vigenére systemet vælger man en række hele tal, som skrives under meddelelsens bogstaver, idet den valgte talrække gentages, hvis antallet af bogstaver i meddelelsen er længere end talrækken. Hvert bogstav kodes så ved at erstatte det med det bogstav, der står lige så mange pladser længere fremme i alfabetet, som det tilhørende tal angiver.

A	N	G	R	I	B	N	U
3	7	20	0	3	7	20	0
D	U	Ø	R	L	I	A	U

Der er ikke let at bryde Vigenére systemet, men kender man længden af talrækken, perioden, så er det ganske simpelt. En nøje statistisk analyse afslører, at visse karakteristiske træk ved sproget ikke lader sig skjule ved krypteringen, og dette kan føre til bestemmelse af perioden blot teksten er 5 - 10 gange længere end perioden.

Det victorianske internet

Med telegrafens fremkomst i midten af 1800-tallet opstår helt nye behov for sikkerhed, og de samme diskussioner, vi har i dag med hensyn til sikkerhed på internettet, var på dagsordenen dengang.

I princippet kan enhver jo tappe en telegraflinje, hvad den danske regering så bitterligt måtte sande i forbindelse med fredsslutningerne i Wien efter 1864-krigen. Her sendte man meddelelser fra København til Wien via Berlin. Den anvendte kode var ikke mere kompliceret end Cæsars, så det voldte ikke Bismarck større problemer at læse med.

Med Cæsar og Vigenére systemet klarede man krypteringen med blyant og papir, men efterhånden som behovet for kryptering blev større, udvikledes alskens sindrige instrumenter hertil, fx de berømte maskiner fra 2. Verdenskrig, Enigma og Hägelin.

Moderne krypteringsmetoder

I 1977 udviklede Rivest, Shamir og Adleman et krypteringssystem, der gav langt større sikkerhed end tidligere og var velegnet til computere. Princippet i selve krypteringsdelen i RSA-systemet er følgende: Teksten omsættes til tal ved for eksempel først at kode hvert bogstav således

A = 01,  B = 02,  . . .  ,  Å = 29

Den kodede tekst kan derefter inddeles i blokke, så hver blok er et tal m med for eksempel 150 cifre. Den maksimale størrelse af m må højst være lig med et på forhånd valgt naturligt tal n. I figuren nedenfor er der brugt blokke på 6 cifre.

ANG	RIB	VED	DAG	GRY
011407	180902	220504	040107	071825
m 1	m 2	m 3	m 4	m 5

Det er forbavsende enkle beregningsformler, der bruges til at kryptere blokkene. Der vælges et passende naturligt tal k, og hver blok m krypteres ved at udregne den rest man får, når m ^k divideres med n. Dette tal betegnes rest(m ^k, n ).

Eksempel Hvert enkelt bogstav krypteres altså ikke for sig, men for at illustrere princippet, er valgt et n på 33. Når k samtidig sættes til 3, bliver krypteringen som vist i tabellen.  Fx er 93 = 729 = 22 · 33 + 3        så           rest (93, 33) = 3 Det er afgørende, at tallene i anden kolonne er de samme som i første kolonne, blot i en anden rækkefølge, hvilket ikke vil være tilfældet for alle værdier af k. Man kan dekryptere på samme måde som man krypterede, men med en anden værdi for k. Denne værdi - der normalt kaldes d - kan i eksemplet vælges som 7. Fx er 37 = 2187 = 66 · 33 + 9       så          rest (37, 33) = 9 og så er man tilbage. m 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 rest(m3,33) 1 8 27 31 26 18 13 17 3 10 11 12 19 5 9 4 m 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 rest(m3,33) 29 24 28 14 21 22 23 30 16 20 15 7 2 6 25 32

Krypteringen er bestemt ved talparret (k,n ), som derfor kaldes en nøgle, og man kan som i eksemplet få den oprindelige meddelelse frem ved at bruge en nøgle (d,n ) på den krypterede meddelelse.

Selvom beregningsformlerne er enkle, er det klart, at regning med så store tal som dem der bruges i praksis, kræver en computer og specialprogrammer. Tænk på at skulle opløfte et tal på omkring 100 cifre til en potens, hvor eksponenten for eksempel har 20 cifre.