Public Key – konceptet

I de konventionelle systemer er der ingen principiel forskel på at kryptere og dekryptere. Kan man det ene, kan man også det andet.

I Cæsars system krypteres ved at forskyde 3 pladser til højre i alfabetet - der dekrypteres ved at forskyde 3 pladser til venstre.

I RSA-systemet er det ikke i praksis muligt at dekryptere en tekst, selvom man kender den nøgle (k,n ), der er brugt ved krypteringen. I dette system vælges n som et produkt af to primtal, og det er kun muligt at bestemme den nøgle (d,n ), der kan dekryptere, hvis man ved, hvilke to primtal n er dannet udfra.

Det er nemt nok at opløse et tal n i primfaktorer ved at prøve sig frem, hvis n ikke er for stort, men for tal med 150 cifre bliver det en helt uoverkommelig opgave for selv de allerhurtigste computere. For den, som kender de to primtal, som n er produkt af, er det til gengæld ret let at beregne d, men fremgangsmåden er en teknisk detalje.

En person kan altså selv konstruere en nøgle (k,n ) og offentliggøre den på for eksempel sin hjemmeside og bede om at vigtige meddelelser bliver krypterede med denne nøgle. Selv om en af disse meddelelser skulle blive opsnappet af en fjende, vil fjenden ikke kunne dekryptere den, da det kræver kendskab til nøglen (d,n ). I en sådan situation kaldes (k,n ) den offentlige nøgle, som også betegnes P (for public), mens (d,n ) kaldes den hemmelige nøgle, som betegnes S (for secret).

De to nøgler ophæver hinanden forstået på den måde, at hvis man låser, det vil sige krypterer, med for eksempel den hemmelige nøgle, så kan man låse op, altså få den oprindelige tekst frem, med den offentlige nøgle. Den nøgle, der er brugt til at låse, kan ikke, i modsætning til en almindelig nøgle, låse op igen.

Digital signatur

Der kan også være behov for, at man som afsender af en meddelelse, ikke nødvendigvis hemmelig, kan godtgøre, at man virkelig er den, man giver sig ud for at være. Hvis man har en hemmelig nøgle S og en offentlig nøgle P, kan man sammen med den egentlige meddelelse sende en typisk kortere tekst H, dels i en ikke krypteret udgave, dels i en udgave S(H), der er kryp-teret med den hemmelige nøgle. Modtageren kan så bruge den påståede afsenders offentlige nøgle P på S(H) og se efter om man får H. Det er jo kun, hvis de to nøgler svarer til hinanden, at man får den oprindelige tekst H frem. Afsenderen kan på denne måde sætte sin underskrift på meddelelsen, sin digitale signatur.

Hvor skal den enkelte bruger af et public-key system anbringe sin offentlige nøgle, således at de andre brugere har adgang til den og kan være sikre på, at den virkelig tilhører den person, som påstås at være ejermanden?

I Danmark vandt TDC i 2003 Videnskabsministeriets udbudskonkurrence om Digital Signatur. Det betyder, at TDC registrerer offent-lige nøgler og garanterer for ejernes identitet. Når en bruger registreres udstedes et såkaldt personcertifikat, og aftalen mellem staten og TDC betyder, at disse certifikater er gratis, og at alle kan få et personcertifikat, uanset om man er kunde hos TDC eller ej.

Sikkerheden

Sikkerheden i et public-key system bygger på, at man ikke kan dekryptere en meddelelse, selvom man kender krypteringsnøglen (k,n ). Man kan forestille sig, at en fjende ville kunne angribe systemet på en række forskellige måder.

Man kan jo i princippet få den oprindelige tekst frem ved at løse ligninger af typen

r = rest(x^k,n) fx 5 = rest(x³,33)

Det vil tage for lang tid bare at prøve sig frem ved at indsætte 1, 2 , … osv. som x, når n er tilstrækkelig stor.

Der er heller ikke fundet mere avancerede brugbare søgningsmetoder, som ved almindelige ligninger, hvor man ved indsættelse af et gæt kan sammenligne venstresiden og højresiden og på den måde se, om man er i nærheden af en løsning. Det hænger sammen med at højresiden varierer så tilfældigt som vist på figuren.

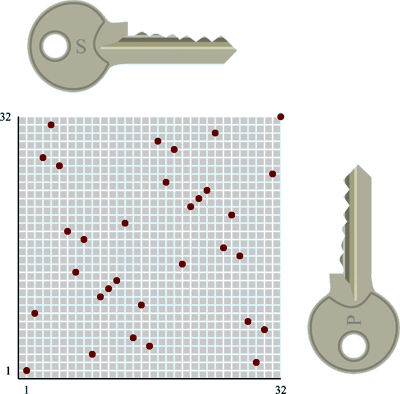En tekst, der er krypteret med denne funktion, skal dekrypteres ved at bruge den omvendte funktion, hvor man for en given y-værdi finder den tilsvarende x-værdi.

Systemet ville som nævnt også kunne angribes ved (at prøve) at faktorisere n, altså finde de to primtal, som n er et produkt af. Det er utænkeligt, at selve computerens hastighed skulle kunne øges så meget, at dette skulle kunne lykkes med de nuværende kendte matematiske metoder; men det er ikke udelukket at der bliver fundet en ny faktoriseringsmetode, der er langt hurtigere end de kendte.

Matematiske opdagelser når sjældent avisforsiderne, men det skete i efteråret 2002. Det var lykkedes tre indiske matematikere Agrawal, Kayal and Saxena at finde en ny test til at afgøre, om et tal er et primtal. Testen, der i dag kaldes AKS-algoritmen er forbavsende enkel og teoretisk set hurtigere end tidligere kendte test.

Nogle af de første pressemeddelelser om den nye primtalstest antydede at den kunne være en trussel mod RSA-systemet; men det er ikke tilfældet. Snarere tværtimod. Den gør det lettere at finde de primtal, der skal bruges til at lave n, men har ingen indflydelse på faktoriseringen af n. Når matematikere har kunnet overse en så simpel primtalstest så længe, kunne de måske også have overset en simpel faktoriseringsmetode.

Firmaet Cryptomathic, hvis logo ses ovenfor, udvikler sikkerhedssystemer til kommunikation via nettet. Det blev startet i 1986 af tre matematikere fra Århus, og har udviklet sig til en større virksomhed med kontorer i flere lande i Europa. I Danmark har TDC benyttet software fra Cryptomathic ved udviklingen af systemet til digitale signaturer.