Statistik - viden eller tilfældighed

Test af hypoteser

I 1996 offentliggjorde Henrik Møller en artikel i The Lancet, hvor han gjorde opmærksom på, at der er tegn på, at der efter 1951 fødes færre og færre drenge i forhold til piger. Analysen byggede på tallene i nedenstående tabeller, som er offentligt tilgængelige:

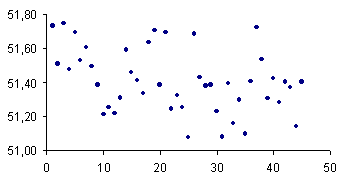
I det følgende betegner x antal år efter 1951, og y procent drengefødsler det pågældende år.

Et plot af punkterne (x, y) viser måske nok en faldende tendens, men ikke mere end, at man nok synes, at det kunne skyldes tilfældige udsving.

Hvis der ikke sker nogen ændring i sandsynligheden for at få en dreng i perioden fra 1951 til 1995, kan de 45 observationer stort set (NB antal fødsler varierer noget) opfattes som resultater af gentagelser af samme eksperiment. Et eksperiment, der giver resultater med en middelværdi på ca. 51,4 og en spredning på ca. 0,2. Den vandrette linie, der går gennem middelværdierne for hvert år, kaldes den sande regressionslinie, og den vil altså have hældningen 0.

Vi vil finde ud af, hvordan hældningerne fordeler sig for regressionslinier til et stort antal simulerede observationssæt, ved hjælp af et program på TI-83 , der er vist nedenfor:

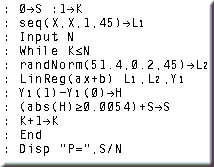
I hvert af årene 1 til 45 (svarende til 1951 til 1995) vælger lommeregneren tilfældigt et tal fra en normalfordeling med middel 51,4 og spredning 0,2. Disse tal lægges i L₂ og årene lægges i L₁. Antallet af observationssæt kaldes N, og H er hældningen af en simuleret regressionslinie.

Programmet giver en P-værdi, der siger, hvor ofte den simulerede hældning har været under -0,0054 eller over 0,0054.

Når man skal vurdere P-værdien bruger man normalt følgende regel:

1. Kør programmet med for eksempel N lig med 100 (det tager ca. 10 minutter), og lav en passende konklusion.
2. Man kan godt lave andre, mere enkle tests: hvis y_x betegner andelen af drengefødsler x år efter 1950, kan man se på forskellene d_x = y_x+23 - y_x. Ved optælling ses, at 7 ud af 22 forskelle er negative. Antallet af negative differenser kaldes D. Hvis det er rigtigt, at der ikke sker nogen ændring i sandsynligheden for at få en dreng, skulle man forvente lige mange negative og positive differenser.
3. Beregn 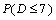under forudsætning af, at sandsynligheden for en negativ differens er 0,5. Hvad ville man konkludere på baggrund af dette test med hensyn til, om der sker ændring af sandsynligheden for at føde en dreng.
4. I ovenstående test udnytter man ikke den information, der ligger i differensernes størrelse, man ser kun på fortegnet. Lav et plot af differenserne i for eksempel Excel. Viser dette plot tegn på, at der sker ændring af sandsynligheden for at føde en dreng?