Der findes ikke nogen formel til at finde for eksempel primtal nummer 1000 uden at bestemme de foregående, men der er heller ikke nogen enkel metode til bare at afsløre om et tal er et primtal. Vi vil her se på den mest nærliggende metode, nemlig at forsøge at finde divisorer fra neden af.
Opgaverne er formuleret under forudsætning af, at der er en TI-83 lommeregner til rådighed; men opgaven kan nemt tilpasses en CAS lommeregner eller et computerprogram.
Lommeregneren har indbygget funktionen int(x ), der beregner den hele del af x, altså det største hele tal mindre eller lig x. Ved hjælp af denne funktion kan rest(n,k ) beregnes som
Dette udtryk indgår i følgende program PrgmPRIM, der finder ud af om et givet tal N er et primtal, ved at undersøge om nogen af tallene fra 2 til kvadratroden af N går op i N.
: Input "N = ",N
: For (K,2,Int(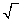 (N))) (N)))
: If N-K*int(N/K)=0
: Then : Disp "NEJ"
: Goto A
: End : End
: Disp "JA"
: Lbl A
|
| 1. |
Undersøg hvor lang tid det tager lommeregneren at køre programmet for hver af følgende værdier af N:
| 1009 |
10007 |
100003 |
1000003 |
10000019 |
og opstil ud fra disse tal en sammenhæng mellem antal cifre og tid. Sammenlign den tid, det ville tage at undersøge et tal med 200 cifre, med universets alder, som anslås at være 14 · 109 år.
|
| 2. |
Udled teoretisk en sammenhæng mellem antal cifre og tid. |
Metoden i programmet er i raffineret form Eratosthenes si (240 f.kr.). I talrækken:
2 , 3 , 4 , 5 , 6 , 7 , 8 , 9, .... , n
udtages det mindste tal 2 og alle egentlige multipla af 2 bortsies:
3 , 5 , 7 , 9 , 11, … , n
dernæst udtages 3 i listen og alle egentlige multipla af det 3 bortsies:
Således fortsættes succesivt med at udtage det mindste tal i listen og bortsi egentlige multipla heraf. Når processen standser, har vi udtaget alle primtal mindre end eller lig n. Metoden kan afprøves i praksis for n = 400 på
|
|