Opgave 4
For at kunne forstå ideen i AKS-algoritmen får man brug for at
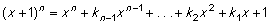 |
(6) |
hvor koefficienterne k i er hele tal, der ifølge binomialformlen kan udregnes som
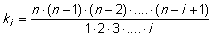 |
(7) |
| 1. |
Udregn (x+1)4 og (x+1)5 ved (6) og (7). |
Der gælder følgende primtals kriterium:
|
Tallet n er et primtal, hvis og kun hvis n går op i samtlige koefficienter i polynomiet
|
|
(8) |
| 2. |
Gør rede for at ovenstående påstand er rigtig. |
Dette elegante primtals kriterium er imidlertid slet ikke til beregningsmæssig nytte. For store n er det umuligt at beregne (x+1)n. Ideen er nu istedet at beregne resten r (x) af 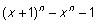 ved polynomiers division med polynomiet x r - 1 for et passende r. Denne rest kan beregnes ved brug af regnereglerne (2) og (3) uden at behøve beregne (x+1)n . Samtidigt gælder (8) i en vis forstand næsten, når ved polynomiers division med polynomiet x r - 1 for et passende r. Denne rest kan beregnes ved brug af regnereglerne (2) og (3) uden at behøve beregne (x+1)n . Samtidigt gælder (8) i en vis forstand næsten, når 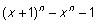 erstattes med r (x), som det antydes af eksemplet i de følgende opgaver: erstattes med r (x), som det antydes af eksemplet i de følgende opgaver:
| 3. |
Når r =2 er det muligt at bestemme r (x ) uden at lave divisionen. Sæt 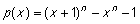 . Gør rede for, at r (x) er et førstegradspolynomium, hvis graf går gennem (-1, p(-1)) og (1, p(1)) og at . Gør rede for, at r (x) er et førstegradspolynomium, hvis graf går gennem (-1, p(-1)) og (1, p(1)) og at 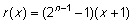 når n er ulige. når n er ulige. |
| 4. |
Gør rede for at n går op i koefficienterne i r (x), hvis n er et primtal. |
Der findes desværre n, der ikke er primtal, for hvilke n går op i samtlige koefficienter i polynomiet 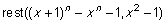 . Det mindste er 341. Men metoden kan reddes ved så at se på rest ved division med . Det mindste er 341. Men metoden kan reddes ved så at se på rest ved division med 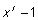 for større primtal r end 2. Vi stopper imidlertid her, hvor hovedideen i AKS-algoritmen er illustreret. for større primtal r end 2. Vi stopper imidlertid her, hvor hovedideen i AKS-algoritmen er illustreret.
| 5. |
Udregn rest(2340,341) ved at bruge 210 som mellemstation. |
Det afgørende ved AKS-algoritmen er, at tidsforbruget ikke vokser eksponentielt som funktion af antallet af cifre, men som en potensfunktion (eller polynomium).

|
|
![]() ved polynomiers division med polynomiet x r - 1 for et passende r. Denne rest kan beregnes ved brug af regnereglerne (2) og (3) uden at behøve beregne (x+1)n . Samtidigt gælder (8) i en vis forstand næsten, når
ved polynomiers division med polynomiet x r - 1 for et passende r. Denne rest kan beregnes ved brug af regnereglerne (2) og (3) uden at behøve beregne (x+1)n . Samtidigt gælder (8) i en vis forstand næsten, når ![]() erstattes med r (x), som det antydes af eksemplet i de følgende opgaver:
erstattes med r (x), som det antydes af eksemplet i de følgende opgaver:![]() . Det mindste er 341. Men metoden kan reddes ved så at se på rest ved division med
. Det mindste er 341. Men metoden kan reddes ved så at se på rest ved division med ![]() for større primtal r end 2. Vi stopper imidlertid her, hvor hovedideen i AKS-algoritmen er illustreret.
for større primtal r end 2. Vi stopper imidlertid her, hvor hovedideen i AKS-algoritmen er illustreret.